电子世界的“记忆魔法”：RC电路如何让信号变得有“频率”？

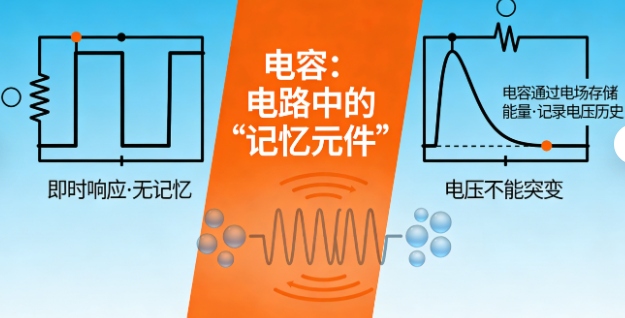
当你从直流电路的稳态世界，迈向信号千变万化的交流领域时，一种神奇的基础电路立刻会成为你必须掌握的核心工具——那就是RC电路。仅仅由一个电阻（R）和一个电容（C）组合而成，它的结构简单到令人惊讶，但所展现的行为却复杂而迷人，堪称模拟电子学中一道分水岭。这一切奥妙的起点，都源于电路中那个关键的“记忆元件”：电容。与电阻这类“即时响应”的元件不同，电容拥有一种独特的能力——它能“记住”自己近期的电压历史。当你试图给一个电容充电或放电时，它不会像电阻那样立即建立起电流与电压的线性关系；相反，它会表现出一种“惰性”，其两端的电压不能突变，只能随着电荷的累积或释放而连续、平滑地变化。这种“抵抗电压变化”的特性，本质上就是它在利用电场存储能量，记录下施加于其上的电压“过往”。正是这种记忆历史的能力，赋予了RC电路以时间维度，让它从简单的分压器，演变成了能够区分信号快慢、塑造信号波形的关键角色。

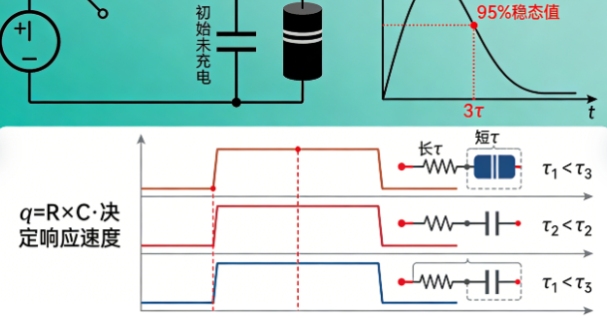
那么，当电阻和电容携手合作，究竟会发生什么？设想一个最简单的场景：一个直流电源通过一个电阻，对一个初始未充电的电容充电。在开关闭合的瞬间，由于电容“记住”自己电压为零的状态，它会表现得像一个短路，此刻充电电流最大。随着电荷不断累积，电容电压缓慢上升，它“记住”的电压值越来越高，反过来抵抗电源的倾向也越来越强，导致流过电阻的充电电流逐渐减小。这个过程并非瞬间完成，而是遵循着一条优美且可预测的指数曲线。决定这条曲线上升速度的，便是大名鼎鼎的RC时间常数（τ = R × C）。它就像一个内在的时钟，τ越大，电容充放电越慢，记忆效应越持久；τ越小，响应则越快。这个简单的时间常数，是理解一切RC电路动态行为的基石。

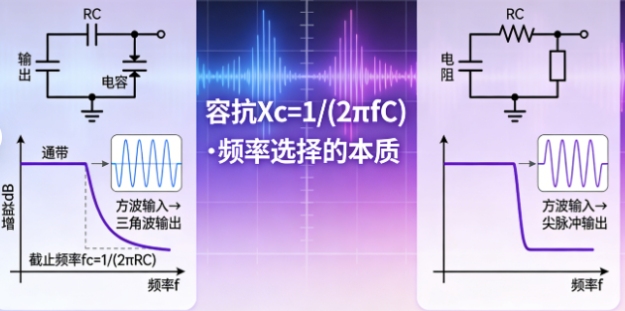
而RC电路真正大放异彩、展现其“魔力”的地方，在于它对不同频率信号的差异化响应，这让我们进入了频域分析的精彩世界。当一个幅度恒定但频率不断变化的正弦波电压信号加在RC电路上时，奇妙的现象发生了：电路输出的信号幅度和相位，将不再恒定，而是与输入信号的频率密切相关。对于由电阻和电容串联构成的分压电路，如果从电容两端取输出电压，我们会得到一个低通滤波器：低频信号能够几乎无衰减地通过（因为电容对缓慢变化的电压呈现出高阻抗，类似开路），而高频信号则会被大幅衰减（因为电容对快速变化的电压呈现出低阻抗，类似短路）。反之，如果从电阻两端取输出电压，便得到了一个高通滤波器。这种频率选择特性，正是利用了电容的阻抗随频率变化（容抗 Xc = 1/(2πfC)）这一根本性质。电容以其“记忆”特性，在时域中创造了时间延迟，映射到频域中，就表现为对不同频率成分的过滤与整形。从平滑电源波纹的滤波电路，到决定数字电路响应速度的延时电路，再到音频设备中的音调控制，其核心原理都离不开RC电路这种基础的频率依赖行为。

掌握RC电路的分析，有两种强大而互补的工具：时域分析和频域分析。时域分析关注电压电流随时间变化的曲线，通过求解微分方程，我们能精确预测电容上电压从一种状态过渡到另一种状态的完整过程，例如方波通过RC电路后如何被“磨圆”了棱角，变成了近似锯齿波或三角波。而频域分析则通过“复阻抗”的概念，将电容视为一个与频率有关的复数阻抗，利用类似直流分压定理的方法，轻松计算出电路在不同频率下的增益和相位偏移，这对于理解和设计滤波器至关重要。这两种视角，如同经纬线，共同编织出我们对RC电路行为的完整认知图谱。

从理解电容的“记忆”起步，到掌握RC时间常数，再到领悟其频率筛选的奥秘，学习RC电路的过程，是一段从静态思维迈向动态思维的旅程。它不仅是分析更复杂的运算放大器电路、谐振电路乃至数字系统的基础，更是在培养一种重要的工程直觉：如何看待和处理随时间变化的信号。每一个精心设计的RC环节，都可能是在为信号“提速”或“减速”，是在“保留”其低吟或“剔除”其尖啸。在这个由电阻和电容构筑的简单世界里，蕴藏着处理真实世界连续信息的最原始也最核心的逻辑。下一次当你看到这两个不起眼的元件并肩而立时，希望你能想起，它们正静静地上演着一场关于时间、记忆与频率的静默戏剧。